Class test economics grade XI

 

Ques - The runs scored by 11 players in the cricket match are as follows:     (1)

7, 16, 121, 51, 101, 81, 1, 16, 9, 11, 16

Find the median of the data.

Ques - For any given data, the mean is 45.5, and the median is 43. Find the modal value. (3)

Ques - Find correlation coefficient:           (4)

Ques - Find the mode of the following data distribution:     (4)

Class-Interval	10-20	20-30	30-40	40-50	50-60
frequency	12	35	45	25	13

Ques - Calculate the median from the following data:             (4)

Rent (In Rs.)	15 – 25	25 – 35	35 – 45	45 – 55	55 – 65	65 – 75	75 – 85	85 – 95
No. of houses	8	10	15	25	40	20	15	7

Ques - Calculate the coefficient of rank correlation from the following data:    (4)

X	48	33	40	9	16	16	65	24	16	57
Y	13	13	24	6	15	4	20	9	6	19

Ques - The runs scored by 11 players in the cricket match are as follows:     (1)

7, 16, 121, 51, 101, 81, 1, 16, 9, 11, 16

Find the median of the data.

Solution:

Given data: 7, 16, 121, 51, 101, 81, 1, 16, 9, 11, 16.

Now, arrange the data in ascending order, we get

1, 7, 9, 11, 16, 16, 16, 51, 81, 101, 121.

Here, the number of observations is 11, which is odd.

Thus, median = 6th term

Hence, the median of the given data is 16.

Ques - For any given data, the mean is 45.5, and the median is 43. Find the modal value. (3)

Solution:

We know that, 

Mode = 3 Median – 2 Mean 

∴ Mode = 3 × 43 – 2 × 45.5 

= 129 – 91 = 38. 

Mode = 38.

Ques - Find correlation coefficient:           (4)

Answer:
The table below shows the calculations required to find correlation coefficient between cost and supply.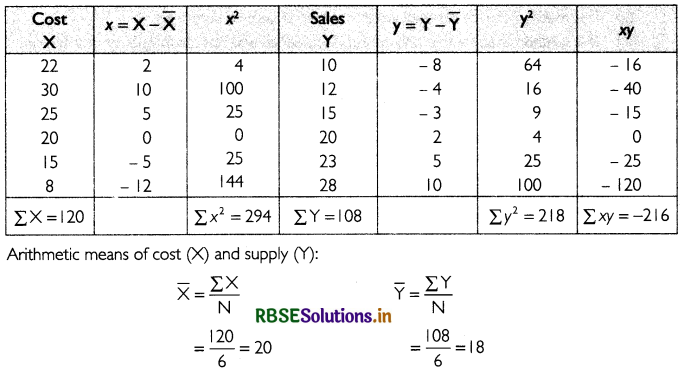


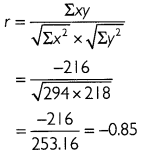
Thus, the correlation coefficient between cost and supply is - 0.85.

Ques - Find the mode of the following data distribution:     (4)

Class-Interval	10-20	20-30	30-40	40-50	50-60
frequency	12	35	45	25	13

Solution:

Clearly, the modal class is 30-40, then 

l = 30 

fk = 45 

fk – 1 = 35 

fk + 1 = 25 

h = 40 – 30 = 10 

= 30 + [(45 – 35)/(2 × 45 – 35 – 25)] × 10 

= 30 + [10/30] × 10 

= 30 + 10/3 

= 100/3 = 33.333.

Ques - Calculate the median from the following data:             (4)

Rent (In Rs.)	15 – 25	25 – 35	35 – 45	45 – 55	55 – 65	65 – 75	75 – 85	85 – 95
No. of houses	8	10	15	25	40	20	15	7

⇒Median=55+70−5840×10
Simplifying the fractional part on the RHS, we will then get:-
⇒Median=55+284
Simplifying the fractional part further on the RHS, we will then get:-
⇒Median=55+7=62
Hence, the median of the data given is 62.

∴ The required median of the data is 62.

Ques - Calculate the coefficient of rank correlation from the following data:    (4)

X	48	33	40	9	16	16	65	24	16	57
Y	13	13	24	6	15	4	20	9	6	19

ANSWER:

X	Y	R1	R2	D = R1−R2	D2
48 33 40 9 16 16 65 24 16 57	13 13 24 6 15 4 20 9 6 19	8 6 7 1 3 3 10 5 3 9	5.5 5.5 10 2.5 7 1 9 4 2.5 8	2.5 0.5 −3 −1.5 −4 2 1 1 0.5 1	6.25 0.25 9.0 2.25 16 4 1 1 0.25 1.0
					ΣD2=41.00

N = 10

rk=1−6[ΣD2+112(m13−m1)+112(m23−m2)+112(m33−m3)]N3−Nor, rk=1−6[41+112(33−3)+112(23−2)+112(23−2)]1000−10or, rk=1−6[41+2+0.5+0.5]990or, rk=1−0.266⇒rk=0.733
Hence, coefficient of rank correlation = 0.733